关注“金科应用研院”，回复“礼包”

领取风控资料合集

金融机构维持信贷业务的稳定运行，取决于是否能准确评估贷款表现的能力。通过多种方式衡量贷款表现，包括预计因冲销而造成多少损失（Charge offs，即某人未偿还部分或全部贷款）、贷款偿还的速度以及一组给定贷款的每月现金流。如果能准确估计这些值，将会对风险管理中的各种分析和应用都很有帮助。

本文，旨在介绍如何利用量化与数据建模的方法，建立贷款行为状态矩阵和现金流量引擎，实现大规模批量计算贷款现金流，最终科学预测金融机构贷款业务盈利表现。

目录

1. 承保决策
2. 未来现金流量模型
3. 使用梯度提升决策树对贷款转换进行建模
4. 将LTM预测的转换概率转换为现金流量
5. 结论
6. 大规模计算现金流

一、承保决策

宏观政策条件和全球经济季节性对金融机构的业务有很大影响。为了应对这些外部不可控影响，需要金融机构经常调整承保系统的杠杆，以确保可持续地管理外部系统风险。在实际观察新发放贷款的表现之前，预测因承保系统变化而导致的风险损失起着至关重要的作用。

二、未来现金流量模型

出于财务规划和预算的目的，金融机构的财务团队需要准确的了解贷款业务在任何放款月份预计收到的金额。这需要提前一个月、一个季度或一年预测整个贷款组合的每月现金流量。

考虑到财务的需求，需要量化风险管理人员着手构建一个可以回答以下问题的模型：

对于金融机构贷款组合的有限部分，我们期望的还款和现金流量是什么样的？

最初，对这个问题的解决方案是使用历史数据对每个切片的逐月预付款（提前偿还贷款）和损失进行建模。这些分层将贷款分成不同的信用等级、APR 范围和期限长度，将给定分层组内的所有贷款视为同质的（类似资产分池）。

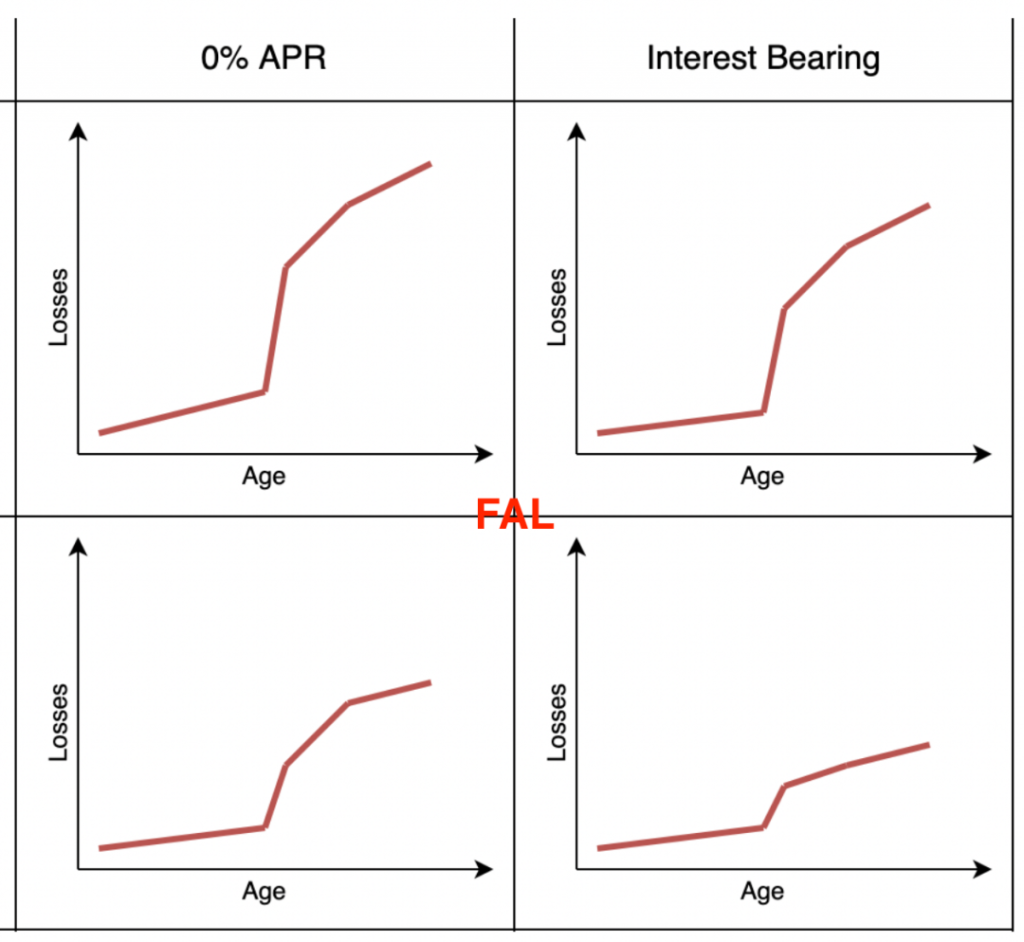
图 1：切片和损失曲线的示例。曲线显示了每个象限定义的贷款的每月损失的本金的预期比例

随着金融机构日益复杂的贷款组合，需要更准确的预测还款。预测模型需要处理越来越多的维度来区分单笔贷款的后续表现。

由于之前的模型将我们限制为有限的贷款分层集，因此对于一笔贷款是任意的、更复杂的实际情况已经不能满足。考虑到这一点，可以将问题重新定义为：

金融机构期望的一笔贷款的还款和现金流量是什么样的？

通过构建贷款转换模型（Loan Transition Model,LTM），并与现金流引擎模型协同工作，使金融机构能够计算任意一组贷款的总消费者还款额，进而可以解决金融机构贷款组合中的每一笔贷款的上述问题。

LTM负责对不同拖欠状态之间的逐月转换概率进行建模，而现金流引擎模型将贷款摊销逻辑应用于消费者的还款行为，以计算还款动态的各个方面，例如本金和利息还款之间的分配。接下来，我将深入为读者朋友们介绍探讨这两部分。

三、使用梯度提升决策树对贷款转换进行建模

在介绍LTM模型预测贷款行为之前，我先为大家科普一下还款行为相关的概念。

贷款行为是指贷款从发起之日到全额偿还或注销之日所经历的过程。如下图：

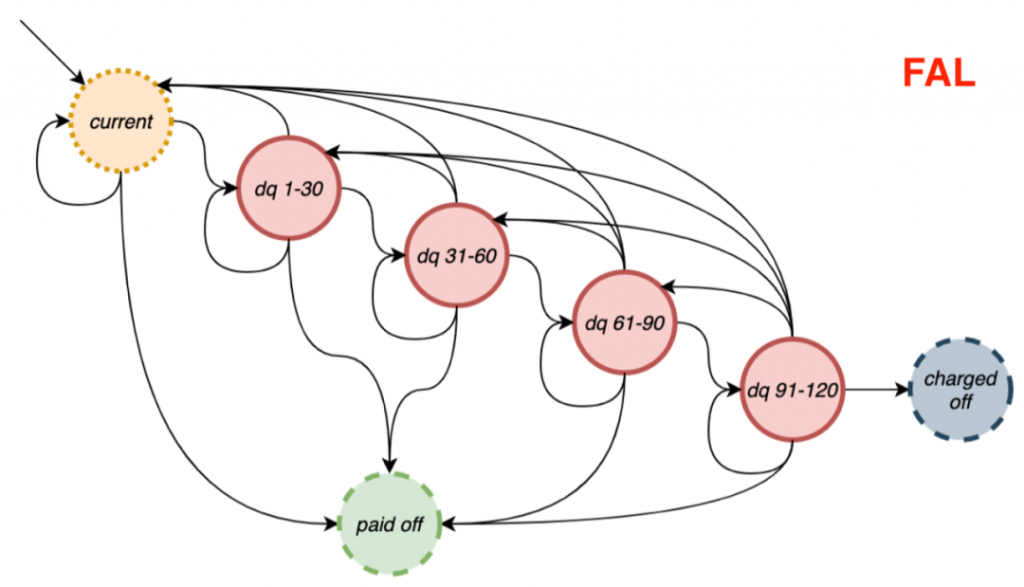
Current：用户已经完成了迄今为止所需的所有付款，这也是新发放贷款的初始状态

dq(n-m)：用户错过了付款，并且延迟了n到m天

charged off：核销/冲销，用户延迟付款超过180天，此时我们假设该贷款出现损失。这是一个终结状态Paid off：贷款已全部还清。这是一个终结状态

LTM模型如下：

表 1：6个月贷款的状态

建立LTM预测前，需要设定一些假设条件：

1. 时间步长单位选取月度，即对逐月发生的贷款状态转换进行建模；
2. 未来转换到不同状态的概率仅取决于当前状态，而不取决于它之前的状态序列（马尔可夫性质）。

综上，LTM预测给定贷款在给定放款月份的状态转换概率。

作为模型的输入特征可以分为自变量和协变量。自变量特征c描述贷款本身，包括分配给贷款的信用评分、贷款金额和期限长度等。协变量特征因贷款状态转换而异，旨在描述每个月的贷款状态。主要的协变量特征是贷款状态s和月份t。该模型输出状态的概率s’，在时间t’ = t + 1，是七个可能的贷款状态中的每一个。更正式地说，它试图预测：

P(s’ = S | c ∩ s ∩ t) for S in {cur, dq1, dq31, dq61, dq91, co, po}

LTM可以生成一个如下所示的转换矩阵：

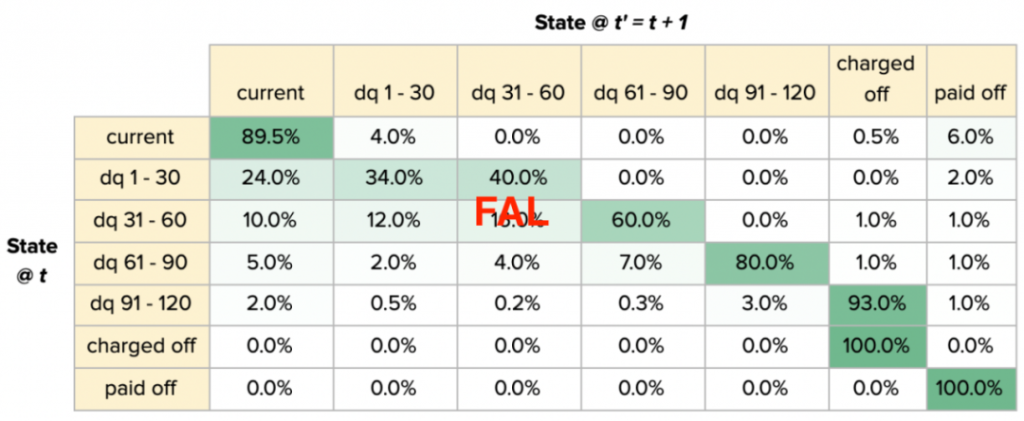
例如，如果在时间t，贷款是当前的，那么模型预测贷款也将在时间t + 1是当前的，概率为 89.5%。由于冲销和付清是最终状态，因此停留在其中的概率为 100%。

该模型本身是一个梯度提升决策树，其中每个类代表一种可能的贷款状态。经过以最小化交叉熵或多类对数损失的模型训练（选择这个损失函数是因为将模型的输出解释为贷款状态的概率分布，如转换矩阵所示），对于金融机构历史记录中的每笔贷款，用于训练模型的数据集每个观察月都有一行。单笔贷款的单个放款月如下所示：

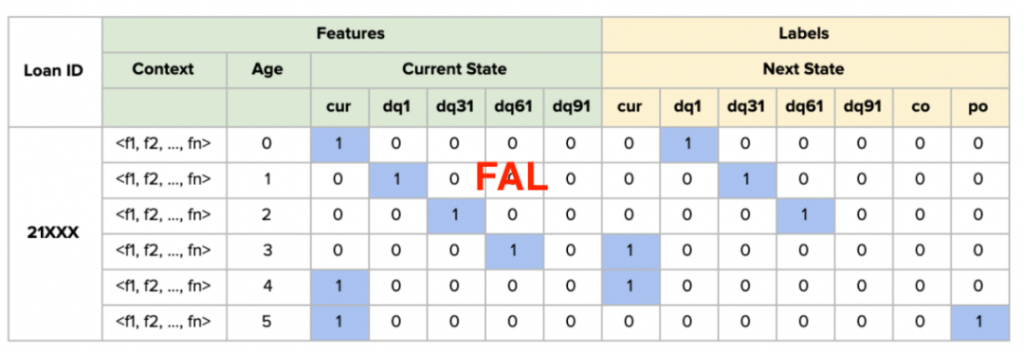
表3：贷款状态链的数据集行

这里要注意的一点，月份t的下一个状态与月份t + 1的当前状态相同。

四、将LTM预测的转换概率转换为现金流量

一旦为给定的贷款计算了一组转换矩阵，对于每个时间月份步长，我们可以使用现金流引擎来计算贷款的不同月度和整体估计，例如支付的利息、支付的本金、本金预付款，本金冲销。这是通过迭代 LTM 的转换矩阵来计算月度概率加权本金余额来实现的。

接下来，通过一个案例来说明这个过程。

案例：跟踪一笔100美元、0%年利率、3 个月贷款的现金流量。从初始概率加权本金余额向量（时间步长t = 0）开始，其中包含当前状态下的所有本金100 美元，因为这是所有贷款的初始状态。

表 4：t=0的概率加权本金余额向量

然后将该向量逐行乘以t = 1转换的转换矩阵，这看起来与表2中的非常相似：

表 5：将初始向量乘以t=1转换矩阵

结果矩阵指定了多少概率加权主体将从每个先前状态转换到每个下一个状态。例如，我们有 $89.50 从current转换到current，代表某人付款，而 $4.00 从current转换到dq 1–30，代表某人错过付款。

下一步是确定在每个状态转换发生后将剩余多少本金。例如，如果我们从current转换到current，这意味着用户已经付款，在本例中为 33.33 美元，因此在此转换后需要偿还的本金金额是现有金额的 0.6667。对于当前到dq 1-30的过渡，无需付款，因此我们将拥有现有金额的 1.0。这些本金余额转换被捕获在我们所说的摊销矩阵中。上一步中的矩阵按元素乘以摊销矩阵，以生成每个付款后的转换概率加权矩阵：

表 6：使用摊销矩阵调整支付的概率加权本金余额

最后，我们对结果矩阵进行列式求和以获得时间步长t=1的概率加权主分布向量。在这种情况下，我们预计当前状态下概率加权余额为59.70美元，t=1时dq 1-30状态下概率加权余额为 4.00美元。让我们继续进行另一次迭代：

我们重复这个过程，直到所有的本金都已经支付，如摊销矩阵所捕获，或者它在冲销和还清状态中累积，因为这些都是最终的。对于计息贷款，我们应用额外的逻辑来计算我们每个月会收取多少利息。最后，我们可以计算许多值，例如：

• 总损失：我们预计在贷款中损失的金额是在冲销状态下剩余的概率加权余额。
• 总现金流：总流入现金流是在还清状态下剩余的概率加权余额加上在贷款期限内支付的所有每月本金和利息的总和。

由于这个迭代过程还为每个中间时间步计算这些值，我们还可以观察这些值如何逐月变化。

五、结论

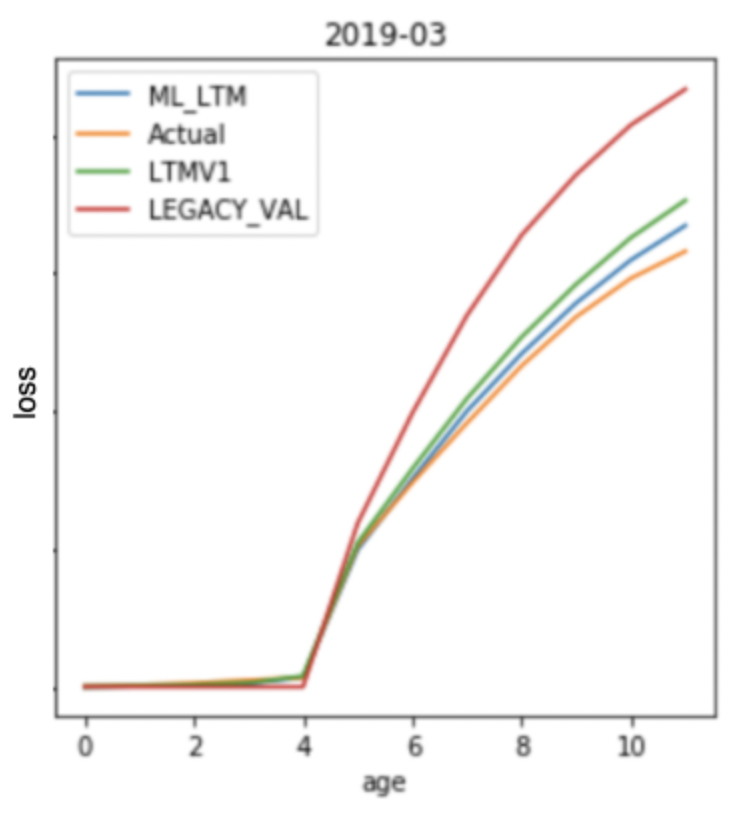
图 3：比较不同方法之间的loss/charge off曲线

从所做的验证来看，很明显基于 LTM 和现金流引擎的方法（ML_LTM 和 LTMV1 曲线）在预测冲销方面比基于切片的方法（LEGACY_VAL 曲线）准确得多。

六、大规模计算现金流

鉴于金融机构需要以批量规模化的方式计算所有贷款的现金流，我们需要训练 LTM 和运行现金流引擎。

什么是大规模批量计算所有贷款的现金流？

假设，我们有n笔贷款并且贷款的平均期限为m，那么我们的训练数据集的大小将为n * m。更重要的是，每个过渡矩阵计算都要求我们使用该模型进行五次预测，每个先前的贷款状态为一次。这样的情景下，在运行现金流引擎时，我们实际上需要5 * n * m 次模型预测。

在金融机构真实场景中，我们使用现金流引擎运行的模拟训练包含数亿笔合成贷款。对于长达 48个月的贷款，我们需要为这些模拟运行数十亿次模型预测。

最终解决方案是，通过将LTM模型训练以及现金流引擎迁移到基于Spark的ML平台来应对这些挑战。

在自建的Spark之上利用XGBoost4J-Spark分布式模型训练，这使我们可以训练可能无法容纳在一台机器上的数据集。此外，在PySpark中实现了现金流引擎的逻辑，以便能够轻松分配上一节中描述的计算。并且能声明性地指定我们为上述任何作业需要多少资源（CPU内核或内存），这使我们可以根据手头的工作量身定制Spark集群的大小，并在将来横向扩展。

参考与致谢

• Anibhav Singla 和 Benson Lee，最初提出 LTM 和现金流引擎。
• Adam Johnston，Hossein Rahimi，建立基础技术架构。
• Wojtek Swiderski，方案最初设计者。

如果你喜欢、想要看更多的干货类型的文章，可以关注公众号【金科应用研院】并设为星标，顺便转发分享～

感谢您看到这里微信公众号【金科应用研院】对话框回复“小福利”，领取粉丝专属优惠券。